I may as well find the equation for these; it would not be fair to the other conics if I only found an equation for a diagonal parabola. Hopefully, the equation for a diagonal ellipse can be expressed as a finite number of functions. Otherwise, the equation could be excessively complicated.

The definition of an ellipse is that for points A and B, the sum of the distances from A to a point on the ellipse and from B to that same point will be constant. A and B are called “foci”.

 

 

If my foci have the same x value, the ellipse will vertical. If my foci have the same y value, the ellipse will be horizontal. I will be giving my foci different x and y values so I have a diagonal ellipse.

I am not going for a generic formula. I am just going to find the ellipse with foci (1,1) and (-1,-1) and with a distance sum of 8. I have no real reason for the distance sum; I’m just hoping that the calculations will be easy. Conveniently, the center of this ellipse is the origin.

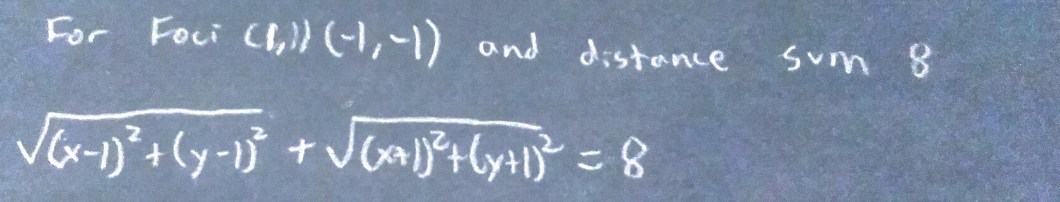
From here, I have to square both sides, then move stuff around, then square both sides again. This will eliminate the square root signs, but I will have x^4 and y^4 terms if I expand everything.

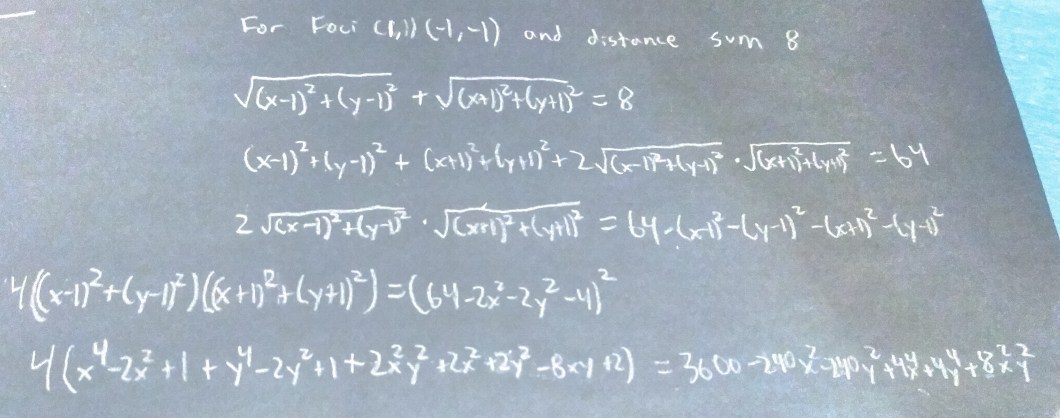
It looks complicated, but if you look closer and examine everything in the last line more closely, you’ll realize that you’re right. This is a nightmare to expand; your math teachers were justified when they chose to teach only horizontal and vertical ellipses.

There are a few silver linings, though. I can eliminate some of the worse terms: x^4, y^4, and x^2y^2. But most of the terms are still there, and because the xy term was not eliminated, this diagonal ellipse seems like it will not be a set of functions. If this is the case, I will not be able to graph this on my calculator.

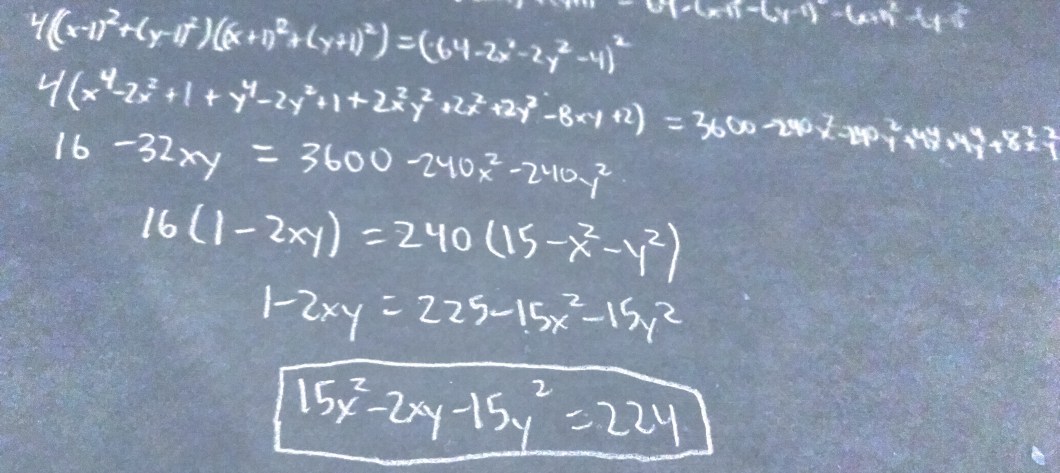
I cannot get this to become a set of functions, but this is the equation of a diagonal ellipse. Because of the shape of an ellipse, I feel safe saying that there is some set of functions that will make this curve, but it is beyond my knowledge. I ran into the same problem as when I tried to find a functional diagonal parabola (in that blog, I did not take into account that I could possibly write a diagonal parabola as two functions, but I still don’t have a clue how to find them).

I am going to try to shift away from conics in the next few posts because any work I do with an ellipse from here will only get more complicated.

Update: my calculus teacher kindly showed me that I can find the equations with the quadratic formula. This can be expressed by two functions, and it does work. I just had a minor lapse of judgement for two weeks.